简介

此模块为学校数据结构必修课学习内容的记录与分享

全文大体分为一下几个部分

• 前言
• 背景
• 分析（伪代码部分）
• 代码
• 结果
• Points

前言

由于前段时间赶团队培训进度，后面需要对培训内容进行总结，因此以后相当一部分时间在 homework 上面的时间可能会减少，因此先贴出主要思路及要点，后面抽时间进行细节补充与整理

又挖坑了…QAQ

背景

• 问题场景：有三根杆子 A、B、C，在 A 杆上从下到上按照大小顺序叠放着 N 个不同大小的圆盘。初始时，所有圆盘都在 A 杆上，B 杆和 C 杆为空。
• 移动规则
  • 每次只能移动一个圆盘。
  • 大盘不能叠在小盘上面。
• 目标：将 A 杆上的所有圆盘借助 B 杆移动到 C 杆上，且移动完成后，圆盘在 C 杆上的叠放顺序与初始在 A 杆上时相同，即从下到上按大小顺序排列。

分析

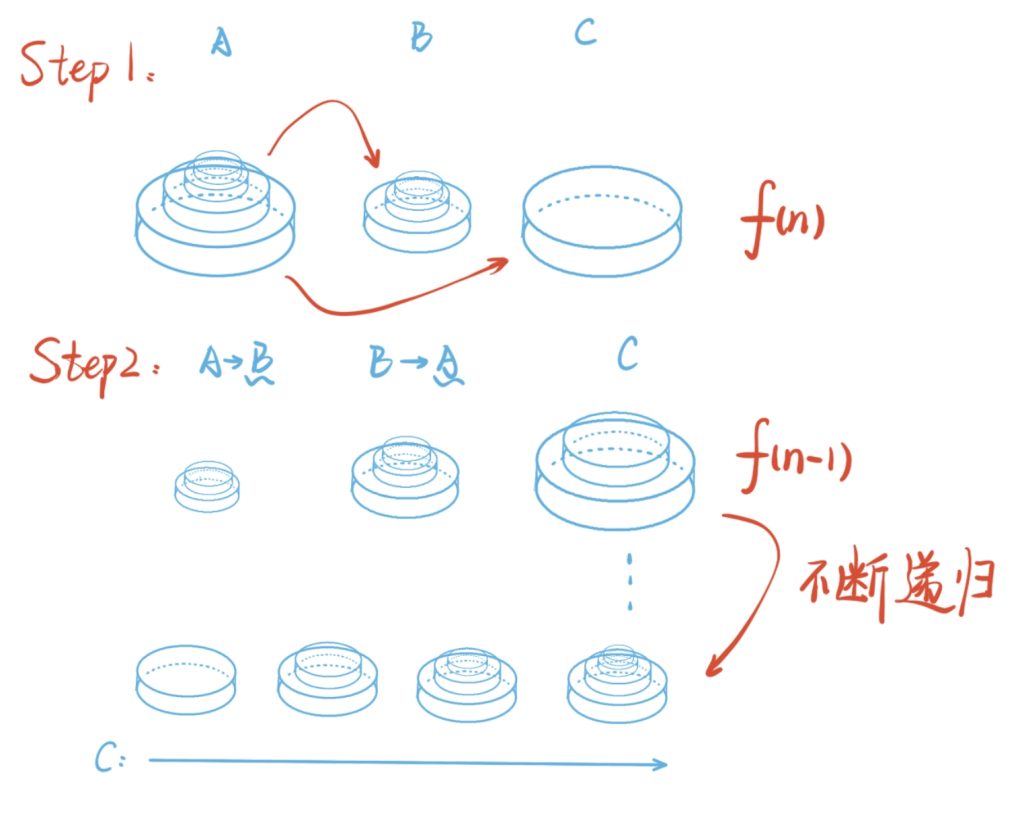
对于每种情况的最后几次操作进行研究，发现：每次都是先把n-1个整体移动到B上，再将最后一个圆盘移动到C上，再将n-1个圆盘移动到C上

如果将每次正确移动到最下面的圆盘忽略掉，那么每次正确执行后，问题就由 f(n) 转化到 f(n-1) 操作上，因此研究的问题具有可递推关系

注意：这里得到的递推函数内部的实参和新参的位置会发生对应改变，这是一个易错点

图示

代码

这个代码比较简单，因此在这里手撕一下

核心函数

void hanoi (int Num, char Begin, char Temp, char End) {
    if (Num <= 0) return;
    if (Num == 1) {
        printf("%c -> %c \r\n",Begin,End);
    }else {
        // 将 n-1 个盘子从a移动到b
        hanoi(Num - 1, Begin, End, Temp);
        // 将剩下一个盘子从a移动到c
        printf("%c -> %c \r\n",Begin,End);
        // 转换参考系。进行下一个hanoi递归操作
        hanoi(Num - 1, Temp, Begin, End);
    }
}

完整代码

#include<stdio.h>

void hanoi (int Num, char Begin, char Temp, char End) {
    if (Num <= 0) return;
    if (Num == 1) {
        printf("%c -> %c \r\n",Begin,End);
    }else {
        // 将 n-1 个盘子从a移动到b
        hanoi(Num - 1, Begin, End, Temp);
        // 将剩下一个盘子从a移动到c
        printf("%c -> %c \r\n",Begin,End);
        // 转换参考系。进行下一个hanoi递归操作
        hanoi(Num - 1, Temp, Begin, End);
    }
}
int main () {
    int num;
    scanf("%d",&num);
    printf("Num=%d\r\n",num);
    printf("the movement:\r\n");
    hanoi(num,'A','B','C');
    return 0;
}

输出

3
Num=3
the movement:
A -> C
A -> B
C -> B
A -> C
B -> A
B -> C
A -> C