简介
此模块为学校数据结构必修课学习内容的记录与分享
全文大体分为一下几个部分
- 前言
- 背景
- 分析
- 代码
- 结果
- Points
前言
由于前段时间赶团队培训进度,后面需要对培训内容进行总结,因此以后相当一部分时间在 homework 上面的时间可能会减少,因此先贴出主要思路及要点,后面抽时间进行细节补充与整理
又挖坑了…QAQ
背景
堆是一种基于完全二叉树结构实现,通常用于优先队列等场景,能高效地获取和调整最值(最大值或最小值)的数据结构;栈是一种遵循后进先出(Last In First Out,LIFO)原则,在函数调用、表达式求值等场景中常用的数据结构,元素的插入和删除操作都在栈顶进行 。
堆和栈在操作系统基本功能以及算法实现等部分具有重要作用,例如:
广度优先搜索(DPF)、括号匹配…
分析
为了实现 后进先出 的目标功能,我们需要一个结构去存储输入和带输出的数据和数据在结构中的相对位置。由于先进先出的数据访问特点,我们不需要太复杂的数据结构 — 使用一维数组即可。
大概的结构体内容:
typedef struct Stack {
int top; // 储存数据在栈[数组]中的相对位置
int stack[Stack_Max_Size]; // 储存数据
}*StackPtr;代码
核心部分
栈可以看作是一个一维遵循先入先出规则的线性数组
#include <stdio.h>
#include <malloc.h>
#define STACK_MAX_SIZE 10
typedef struct CharStack {
int top;
char data[STACK_MAX_SIZE];
} *CharStackPtr;
// 遍历输出栈中的数据【同遍历数组的方式】
void outputStack(CharStackPtr paraStack) {
for (int i = 0; i <= paraStack->top; i ++) {
printf("%c ", paraStack->data[i]);
}
printf("\r\n");
}
// 初始化栈
// 分配空间
// 初始化 top 位置/内容
CharStackPtr charStackInit() {
CharStackPtr resultPtr = (CharStackPtr)malloc(sizeof(struct CharStack));
resultPtr->top = -1;
return resultPtr;
}
// 压栈函数
这里的top++位置和上面的top初始化相关
void push(CharStackPtr paraStackPtr, int paraValue) {
if (paraStackPtr->top >= STACK_MAX_SIZE - 1) {
printf("Cannot push element: stack full.\r\n");
return;
}
paraStackPtr->top ++;
paraStackPtr->data[paraStackPtr->top] = paraValue;
}
// 出栈函数
char pop(CharStackPtr paraStackPtr) {
if (paraStackPtr->top < 0) {
printf("Cannot pop element: stack empty.\r\n");
return '\0';
}
paraStackPtr->top --;
return paraStackPtr->data[paraStackPtr->top + 1];
}
void pushPopTest() {
char ch;
int i;
printf("---- pushPopTest begins. ----\r\n");
// Initialize.
CharStackPtr tempStack = charStackInit();
printf("After initialization, the stack is: ");
outputStack(tempStack);
// Pop.
for (ch = 'a'; ch < 'm'; ch ++) {
printf("Pushing %c.\r\n", ch);
push(tempStack, ch);
outputStack(tempStack);
}//Of for i
// Pop.
for (i = 0; i < 3; i ++) {
ch = pop(tempStack);
printf("Pop %c.\r\n", ch);
outputStack(tempStack);
}//Of for i
printf("---- pushPopTest ends. ----\r\n");
}// Of pushPopTest
void main() {
pushPopTest();
}// Of main图示
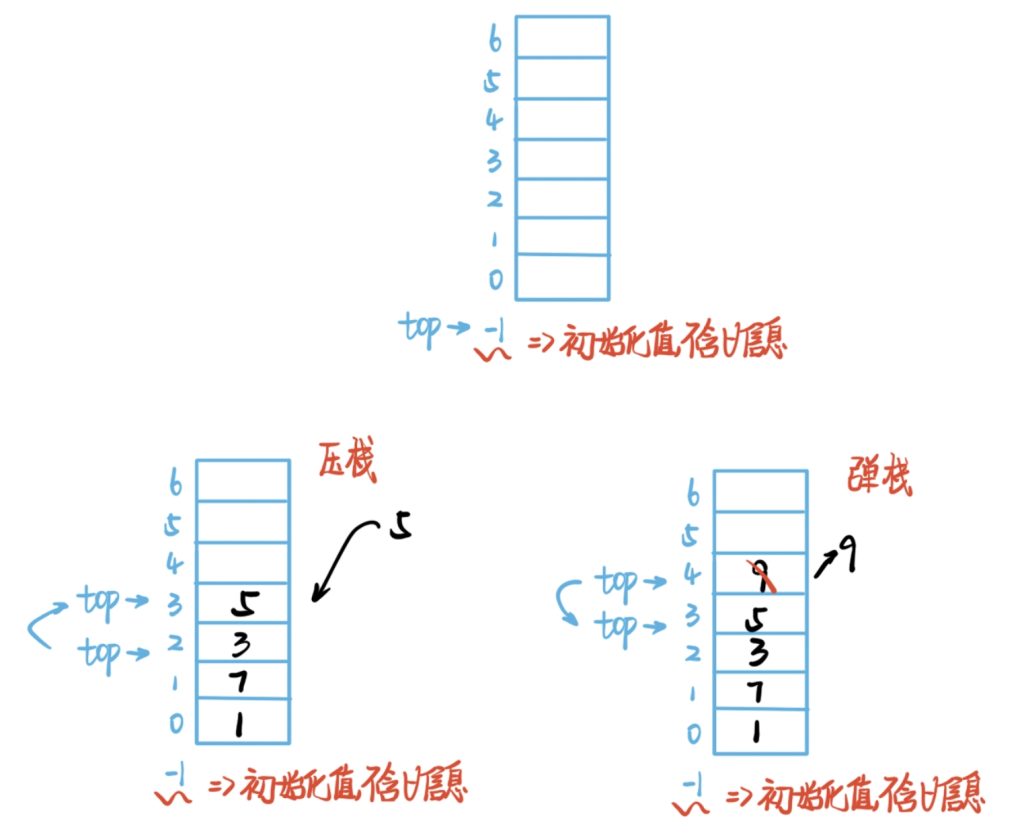
结果
---- pushPopTest begins. ----
After initialization, the stack is:
Pushing a.
a
Pushing b.
a b
Pushing c.
a b c
Pushing d.
a b c d
Pushing e.
a b c d e
Pushing f.
a b c d e f
Pushing g.
a b c d e f g
Pushing h.
a b c d e f g h
Pushing i.
a b c d e f g h i
Pushing j.
a b c d e f g h i j
Pushing k.
Cannot push element: stack full.
a b c d e f g h i j
Pushing l.
Cannot push element: stack full.
a b c d e f g h i j
Pop j.
a b c d e f g h i
Pop i.
a b c d e f g h
Pop h.
a b c d e f g
---- pushPopTest ends. ----
Press any key to continuePoints
top指针到底指向哪里
在
刷题(赶作业)的时候发现下面的一道问题,若是按之前学习的经验来看找不出正确答案,这让我感到十分惊讶。于是我把题目喂给了AI,看到了AI的解释之后恍然大悟:

如此图。在专业课程的学习中,老师讲的是 top 指针指向数组中存储数据的最高位,由此达到弹出后进入栈数据的目的。

从这个点来看,这道题应该是 top[2] – top[1] = 1; 代表栈空间使用完毕才对;
而在AI给出的解释中展示了另外一种指向方式:指向最近的未有储存数据的位置
对于采用顺序存储方式且两栈共享空间
V[1..m]的情况,栈顶指针的相对位置如下:
- 栈 1 的栈顶指针:栈 1 的底在
V[1],其栈顶指针top[1]通常指向栈 1 当前栈顶元素的下一个位置,初始时top[1]=1。随着元素入栈,top[1]会不断增大,当top[1]=m时,说明栈 1 已经到达了共享空间的边界(但不一定栈满,因为还要考虑栈 2 的情况)。- 栈 2 的栈顶指针:栈 2 的底在
V[m],其栈顶指针top[2]指向栈 2 当前栈顶元素的下一个位置,初始时top[2]=m + 1。随着元素入栈,top[2]会不断减小,当top[2]=2时,说明栈 2 已经到达了共享空间的边界(同样不一定栈满,要考虑栈 1 的情况)。当两栈共享空间时,栈满的条件是
top[1]-1 = top[2],此时两个栈顶指针相遇,共享空间被占满。
按照这种假设则选择B项
总结
栈中的 top 指针具有两种指向方式:
- 栈中最后一位元素
- 栈中最后一位元素后的空位
具体选择哪一种看自己的喜好,没有必须的要求
在做题的时候需要注意,如果题目没有进行说明,则两种表示方式均要考虑







