本文最后更新于29 天前，其中的信息可能已经过时，如有错误请发送邮件到zhangweihao22@outlook.com

此模块为学校数据结构必修课学习内容的记录与分享

全文大体分为一下几个部分

背景
分析
代码
结果
Points
概念辨析
易错题本
高质视频推荐

背景

二叉树是每个节点最多有两个子树的树结构，这两个子树分别被称为左子树和右子树。二叉树的子树有左右之分，次序不能颠倒。

二叉树在算法、数据压缩、数据库索引、编译器设计等领域都有重要应用，例如在哈夫曼编码中，通过构建二叉树来实现数据的压缩；在二叉搜索树中，利用二叉树的特性实现高效的数据查找、插入和删除操作。

分析

按照上面的描述，二叉树的结构单元需要具备左右节点指针和数据单元，因此也不难写出其对应结构体：

typedef struct BTtree {
    char data;
    struct BTtree *left;
    struct BTtree *right;
}BTNode, *BTreePtr;

代码

还差一点code

#include<stdio.h>
#include<malloc.h>

#define QUEUE_SIZE 5

typedef struct BTtree {
    char data;
    struct BTtree *left;
    struct BTtree *right;
}BTNode, *BTreePtr;

// 下面采用的是循环队列
typedef struct BTQueue {
    // 可以看作是指针数组，储存一个个树节点
    BTreePtr *NodePtrs;
    int front;
    int rear;
}*BTQueuePtr;

BTQueuePtr InitQueue() {
    BTQueuePtr Q = (BTQueuePtr)malloc(sizeof(BTQueue));
    Q->NodePtrs = (BTreePtr*)malloc(sizeof(BTNode) * QUEUE_SIZE);

    Q->front = 0;
    Q->rear = 1;
    return Q;
}

bool IsEmpty(BTQueuePtr Q) {
    return (Q->front + 1) % QUEUE_SIZE == Q->rear;
}

void EnQueue(BTQueuePtr Q, BTreePtr x) {
    if ((Q->rear + 1) % QUEUE_SIZE == Q->front) {
        printf("Queue is full\n");
        return;
    }// of if
    Q->NodePtrs[Q->rear] = x;
    Q->rear = (Q->rear + 1) % QUEUE_SIZE;
}

BTreePtr DeQueue(BTQueuePtr Q) {
    if (IsEmpty(Q)) {
        printf("Queue is empty\n");
        return NULL;
    }// of if

    // 由初始化两个索引值分别为 0 和 1 ，因此这里必须front先++，再输出数据
    Q->front = (Q->front + 1) % QUEUE_SIZE;
    printf("DeQueue: %c\n", Q->NodePtrs[Q->front]->data);
    BTreePtr x = Q->NodePtrs[Q->front];
    
    return x;
}

BTreePtr ConstructBTreeNode (char data) {
    BTreePtr NewNode = (BTreePtr)malloc(sizeof(BTNode));
    NewNode->data = data;
    NewNode->left = NewNode->right = NULL;
    return NewNode;
}

BTreePtr string2BtreeNode (char *str) {
    int i;
    char ch;
    BTQueuePtr Q = InitQueue();

    BTreePtr ResultHeader;
    BTreePtr TempParent, TempLeftChild, TempRightChild;
    i = 0;
    ch = str[i];
    // 构建根节点
    ResultHeader = ConstructBTreeNode(ch);
    // 将根节点入队
    EnQueue(Q, ResultHeader);
    while (!IsEmpty(Q)) {
        // 从队列中取出一个节点作为当前父节点
        TempParent = DeQueue(Q);

        // 处理左子节点
        i++;
        ch = str[i];
        if (ch == '#') {
            // 如果字符为 #，表示左子节点为空
            TempParent->left = NULL;
        } else if (ch == ')') {
            // 构建左子节点
            TempLeftChild = ConstructBTreeNode(ch);
            // 将左子节点入队
            EnQueue(Q, TempLeftChild);
            // 将左子节点连接到父节点
            TempParent->left = TempLeftChild;
        }// of if

        // 处理右子节点
        i++;
        ch = str[i];
        if (ch == '#') {
            // 如果字符为 #，表示右子节点为空
            TempParent->right = NULL;
        } else if (ch == ')') {
            // 构建右子节点
            TempRightChild = ConstructBTreeNode(ch);
            // 将右子节点入队
            EnQueue(Q, TempRightChild);
            // 将右子节点连接到父节点
            TempParent->right= TempRightChild;
        } // of if
    } // of while
} // of string2BtreeNode

void BFS(BTreePtr root) {
    char TempStr[100];
    int i = 0;
    BTQueuePtr Q = InitQueue();
    BTreePtr TempNode;

    EnQueue(Q, root);

    while (!IsEmpty(Q)) {
        TempNode = DeQueue(Q);
        TempStr[i++] = TempNode->data;

        if (TempNode->left != NULL) {
            EnQueue(Q, TempNode->left);
        }

        if (TempNode->right != NULL) {
            EnQueue(Q, TempNode->right);
        }
    }
    printf("%s\n", TempStr);
    printf("The end : %s",TempStr);
    free(Q);
    free(TempNode);
    free(TempStr);  
    return;
}

int main () {


    return 0;
}

概念辨析

完全二叉树

n-1层都无空缺且n层满足“尽可能左边连续”的二叉树

explanation

你的疑问非常关键，我们来澄清“完全二叉树”的定义，并结合“高度为 8”来严格推理：

✅ 完全二叉树的正式定义是：

对于一个有高度为 hh 的二叉树，
它的前 h−1h – 1 层都是“满的”（即每层节点数为 2层号−12^{层号-1}）；
第 hh 层（最底层）的节点从左到右连续排列，中间不能空缺；
但最底层的节点不一定是满的，只需要是“尽可能左边连续”。

那么问题是：

一个高度为 8 的完全二叉树，最少有多少个叶子结点？

✅ 正确理解高度为 8：

高度为 8，表示有 8 层，最顶层为第 1 层，最底层为第 8 层；
叶子结点只能出现在第 7 层或第 8 层；
如果第 8 层越少，叶子结点就越少；
所以“最少叶子结点”的情形是：第 8 层一个都没有，叶子结点全部出现在第 7 层的末端部分（因为它们没有孩子）。

❗注意：

完全二叉树的最后一层可以不满，所以第 8 层可以没有节点，只要前面满足“完全”的定义就行。

计算：

第 7 层有 26=642^6 = 64 个节点；
如果第 8 层为空，这 64 个第 7 层节点就是叶子；
所以：最少叶子结点数是 64 个。

✅ 结论：

你说的“第八层应该全部有节点”适用于满二叉树，不是完全二叉树。

易错题本

完全二叉树的最大节点数

Q1：已知一棵完全二叉树的第 6层（设根为第1层）有8个叶结点，则该完全二叉树的结点个数最多是

A.39

B.52

C.111

D.119

Q1：对于任意一棵高度为5且有10个结点的二叉树，若采用顺序存储结构保存，每个结点占1个存储单元（仅存放结点的数据信息），则存放该二叉树需要的存储单元数量至少是

A.31

B.16

C.15

D.10

疑问：为什么不能创建一个顺序数据结构来储存信息，这样可以避免空间浪费

高质视频推荐

众所周知，正知识不一定正，但是野知识一定够野

这种应付考试的方法推荐直接掌握如何使用方法，不要浪费时间理解，时间要花在正确的事情上

可视化讲解二叉树的遍历方式

二叉树遍历秒解，前序遍历、中序遍历、后序遍历

二叉树无脑遍历方式

【纯干货】三分钟教会你遍历二叉树！

知二求一【二叉树遍历求解】

这个方法可以帮助求得二叉树的大致构成方式，实际的左右支构成情况还会有多种

无脑秒解！已知先/后序遍历与中序遍历，求后/先序遍历

森林、树、二叉树的无痛转化

【数据结构】树、二叉树、森林直接的转换

计算特定序列顺序二叉树数量

已知节点数，求不同形态的二叉树数量等于求解该数量下的卡特兰数。

而每种形态对应特定序列的二叉树只有一种。因此计算特定序列顺序二叉树数量等价于求解该数量下的卡特兰数。

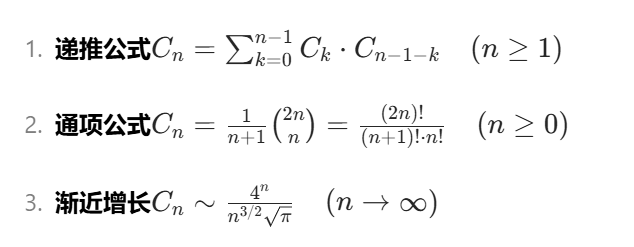
五分钟带你学会树的计数问题（卡特兰数、先序序列和中序序列关系、根据先序序列对应不同二叉树）【408 2015真题数据结构2题】

已知节点数和叶节点数，求无右孩子节点数

已知一棵有 2011个结点的树，其叶结点个数为116，该树对应的二叉树中无右孩子的结点个数是（）。【2011年全国试题6（2分）】

Post Views: 117

背景

分析

代码